面试题:火车运煤问题
 这个可能是一个比较经典的智力题了,和以前的那个《赛马问题》很相似,其题目如下:
这个可能是一个比较经典的智力题了,和以前的那个《赛马问题》很相似,其题目如下:
你是山西的一个煤老板,你在矿区开采了有3000吨煤需要运送到市场上去卖,从你的矿区到市场有1000公里,你手里有一列烧煤的火车,这个火车最多只能装1000吨煤,且其能耗比较大——每一公里需要耗一吨煤。请问,作为一个懂编程的煤老板的你,你会怎么运送才能运最多的煤到集市?
这道题一开始看上去好像是无解的,因为你的火车每一公里就要消耗一吨煤,而到目的地有1000公里,而火车最多只能装1000吨媒。如果你的火车可以全部装下,到目的地也会被全部烧光,一丁点也不剩。所以,很多人的第一反应都是觉得这个不太可能。
如果你一开始就觉得不太可能的话,这是很正常的。不过我不知道你还会不会继续思考下去,如果你不想思考下去了,那么我很为你担忧,因为你可能并不是一个不善于思考的人,而是一个畏难的人,还有可能是一个容易放弃的人。这对于你做好 一个需要大量思考的工作的程序员来说可能并不适合。
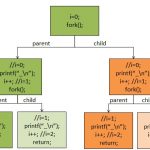
我一开始也觉得不可能,后来想了一想,想到一个解法可以最多运送500吨煤到市场,方法如下:(希望你先自己想一想再查看这个答案)
【查看答案】
好像这样很不错的了,不过还有更好的方法能运更多的媒过去。你知道这个方法吗?可以提示的是,就是以上述这个方法的思路。我先暂时不把答案放上来,你可以自己想想。过两天我把答案放上来。
更新(2011年4月17日):大家都很聪明,533是应该是最优解,大家用了很多种方法阐述了这一过程,我最初的想法和朋友xPacificCoolShell的一致!很高兴看到有更为科学的解法,受教了。另外,还有一些朋友提出火车不能随时随地调头的实际情况,非常不错,所以,以后这题不能用火车运煤了,可能是用马运草更好一点了。;)
(转载本站文章请注明作者和出处 酷 壳 – CoolShell ,请勿用于任何商业用途)






 (50 人打了分,平均分: 4.52 )
(50 人打了分,平均分: 4.52 )
《面试题:火车运煤问题》的相关评论
各位,我昨晚想了很久,但是一直没想到最优解533怎么算的。
首先,我把每段停车的地点记为(
)
昨天想了两个小时,才想到了S(i+1)=S(i)-(2*【S(i)/1000】+1)*(L(i+1)-L(i))这个公式。Li每次停车放煤相对于起点的距离。S(i)是每个停车点最终剩下的煤…
但是一直解就是解不出…
较快算法:
3000吨媒想办法变成2000吨->(3000-2000)/5=200,即分三次运送200公里,现在离终点还剩800公里;
2000吨媒想办法变成1000吨->(2000-1000)/3=333,即分两次运送333公里,现在离重点还剩467公里;
最后一次搞定:1000-467=533;
@守望
这个问题很好理解,因为火车有消耗,所以必须让其尽可能的装满在路上行驶(像资本家剥削工人一样),由3000/1000 = 3知,必须到起点三次;且到第一个中转站时也能使其装满,则必是煤车到此地时有煤2000 车往返五次,(来3回2)第一中转点据地点1000/5=200米,同理第二中转点有煤1000 往返第一中转点三次,距离第一中转点1000/3=333.333米;最后在第二中转点满载到终点。 知道这个原理的话,当有nK吨煤时也很好求解了~~
很好的一道题,但对于本题来说,火车能卸煤的地点一般都是固定的,那么多吨煤在铁轨附近说卸就卸啊。。。
装1000吨煤,走250公里,扔下500吨煤,回矿山。
装1000吨煤,走到250公里处,拿起250吨煤继续向前到500公里处,扔下500吨煤(这里有错,应该是扔下250吨,因为此时火车上只有750吨煤,扔500吨,则会不去了),回矿山。此时火车上还有250吨,再加上在250公里处还有250吨煤,所以,火车是可以回矿山的。
装上最后1000吨煤,走到500公里处,装上那里的500吨煤,然后一直走到目的。
于是,你最多可以运送500吨煤到市场(当然,火车也回不去了,因为那矿山没有煤了)
首先,1/3+1/7 +…+ 1/(2n-1) < 1,所以煤场有再多的煤运到市场也不会超过1吨,所以下面的的解法对煤任意多都是没有问题的,通过这个极限,还可以求出最多能运多少到市场。
coal=3000
left=1000
while (coal != 1000)
{
left -= 1000 / ((coal/1000)*2 – 1); /*消耗1000吨煤能使N吨煤移动的距离*/
coal -= 1000;
}
left就是答案了
@timewalker
这个应该是正解!
不懂为毛大家都说533是最优解。。。
我的思路是这样的:让火车最大负重(1000吨),进行最小消耗(每次只走1公里),那么他就可以卸下998吨,因为还要回城需要1吨煤,所以只能放下998吨。那么每公里火车需要消耗2吨煤,一共1000公里,共需消耗2000吨,最后运到城里的就是3000吨煤。
擦,忘了折返次数了,我这个解题思路应该是消耗煤最多的,5000吨都不够烧的。
一种动态规划的方法
评论里已经有人给出了很简洁的解决方案,下面我想从动态规划的角度给出一种解法:
假设起始运送货物量为 t,终点路程为 s, 火车容量为 c, 可以运抵终点的最多货物量为函数 F(t,s).
在写出递归式前,先列举3种基本情况:(1)t<s: 货物量不足以运送到此距离,所以F(t,s)=0; (2)s<t<c: 火车一次就可以装完货物,所以F(t,s)=t-s; (3)2s<cc使得火车一次无法运完,但因为c>2s,火车可以采用往返的方式多次运输,这种情况下最优的方式就是减少总共往返的次数,也就是直接运到终点而不在中间站卸货,所以F(t,s)=(t/c-1)*(c-2s)+(c-s)
有了这三种基本情况,接着给出递归式: F(t,s) = max{ F( F(t,i) , s-i ) } for all 1=<i<s.
递归式的意思就是,整个问题可以分成两部分,首先从起始点以最优运货量运到位置 i,然后再从位置 i 将当时剩余的货物量以最优方式运到终点。然后再递归的解决两个字问题。至于这个问题是否满足“最优子问题”的准测,大家可以很容易证明。
最后程序结果确实就是大家给出的 533吨。 即先运到200m处,剩余2000吨,再运到533m处,剩余1001吨,最后运到终点,剩余533吨。
我在解的时候把火车可停的位置离散化了,也就是只能停在整数距离上,所以533不一定是最优的,但已经足够接近了。
顺便把python的代码也贴上:
C=1000
T=3000
S=1000
transport=[[0]*(S+1) for i in range(T+1)]
offloadpoint=[[[0,0] for j in range(S+1)] for i in range(T+1)]
#initialize the basic cases
#(1)the basic case:t<=s makes transport near half part are 0's
#(2)for the second basic case
for s in range(1,C):
for t in range(s+1,C+1):
transport[t][s]=t-s
offloadpoint[t][s]=[s,0]
#(3)for the third one
for t in range(C+1,T+1):
for s in range(1,C/2+1):
transport[t][s]=(t/C-1)*(C-2*s)+(C-s)
offloadpoint[t][s]=[s,0]
for s in range(1,S+1):
for t in range(s+1,T+1):
if t<=C or (sC): #either the second or the third basic case
continue
print ‘\r’,t,s,
min_points_num=S
for i in range(1,s):
x=transport[transport[t][i]][s-i]
points_num=offloadpoint[t][i][1]+offloadpoint[transport[t][i]][s-i][1]+1
if x>transport[t][s] or (x==transport[t][s] and points_num<min_points_num):
transport[t][s]=x
offloadpoint[t][s]=[i,points_num]
min_points_num=points_num
print '\n'
print "the maximum amount is ",transport[T][S]
#recursively print out the intermediate offloading points
def print_offloadpoints(amount,src,dst):
point=offloadpoint[amount][dst-src][0]
if point==0:
return -1 #no offload point
elif point==(dst-src):
print src+point,transport[amount][dst-src]
return 0
print_offloadpoints(amount,src,src+point)
print_offloadpoints(transport[amount][point],src+point,dst)
return 1
print_offloadpoints(T,0,S)
@shretju
不知道为啥缩进都没了。
不用切三段这么麻烦,就一点点的走就行。假设不用每次都走一公里,也就是说,走半公里就用0.5吨煤的话:
开始是3000吨煤,每次走一公里要用5吨煤:三次去,两次回。
走到1000/ 5 = 200公里的时候,只有2000吨煤了,这时候每次前进1公里要3吨煤:两次去,一次回。
走到1000/3 = 333.33公里的时候,只有1000吨煤了,直接向前走就行了。
这时候,一共走过了1000/ 5+1000/3=200+333.33=533.33公里。每走1公里要耗费1吨煤,而路程正好是1000公里,所以走过的这些公里就是到最后可以剩下的吨数。是533.33
@无知
left 不是答案,得用1000-left;
首先想到最优解的两个特征:1,火车肯定要从起点出发3次(因为每次最多运1000);2,火车前两次回到起点要用完车上存煤(否则是浪费)。
初步方案:火车前两次都运到某点x,卸下1000-2x,然后用x煤回去,第三次到x点时,车上有1000-x,然后装上x点的煤,若3000-5x不超过1000,直接到终点,用3000-5x=1000的临界条件算得x=400,这也是火车到达终点所剩下的煤。
若3000-5x超过1000,此时与原问题类似,但初始煤变为3000-5x,路程变为1000-x,我们需要选择下一个存煤点,与x点距离y,然后在y点回头一次。
然后想到第三个特征:3,火车回程要尽可能短。使火车回头的原因是火车容量为1000,理想状况为火车每次出发都装满1000的煤,所以火车第三次到达x点时共有煤3000-5x=2000,求得x=200;火车第二次到达y点时站点有存煤1000-2y,火车有煤1000-y,共计2000-3y,理想状况为2000-3y=1000,y=333,火车到达终点剩下煤1000-(1000-x-y)=533。
这题目可以推广为容量k火车要运载Nk煤到距离k点。那么每个中转站点x为N’k-(2N’-1)x=(N’-1)k,N’递减。证明最优解的思路可以从证明火车每次回程最短或者火车每消耗k煤使剩余煤移动距离最远入手。
533完胜
拉三次,第一次的在200位置,因为1000/5,因为来回5次到第一的点.第二次放在333.333位置.因为来回3次到这个点,那第三次到终点剩下533.3333喽.
其实题目还忽略了火车的加速度,如果考虑进去的话可以利用火车的加速度省下不少煤,当然这个说法有点较真,还是马吃草比较无争议。
这个题目有问题吧 难道回程不要烧煤的?好像这里都没提到吧?
刚看到题目也有无解的感觉,一转念觉得有问题,不像看起来那么直接。只要满足几个原则就可以确定解了,题出什么无所谓,问题都一类。
一、火车可掉头。(就能分段拿煤换路程了)
二、从每个节点运出煤都必须无剩余。(哪怕剩余的一点点煤也能使火车带煤向前推进)
三、完成一个节点的运送到达下一节点时。重组装煤时,剩余总煤量应为车载负荷的整数倍。(不出现半车煤起运的情况)
四、满足三原则下,两节点之间消耗的煤应尽量少。(少走2x的路程啊)
原则定出来思路就出来了。
刚看到题目也有无解的感觉,一转念觉得有问题,不像看起来那么直接。只要满足几个原则就可以确定解了,题出什么无所谓,问题都一类。问题很好想,没计算量。结果:分段运,第一个节点在200处,第二个在200 333.33处,答案是533.33。想对了就很简单。
这题想解最优是有运送原则的(如下):
一、火车可掉头。(就能用分段的方式拿煤换路程了,货物煤是可以一点一点装车的,这样才行*^_^*)
二、从每个节点运出煤都必须无剩余。(若剩余,哪怕剩余的一点点煤也能使火车带煤向前推进。浪费!)
三、完成一个节点的运送到达下一节点时。剩余总煤量应为车载负荷的整数倍。(确保再运向下一节点不出现半车煤起运的情况,耗煤代价一样当然要多运才行,半车就运走太不环保了-_-||)
四、满足原则三的情况下,两节点之间消耗的煤应尽量少。(本题就少走2x的路程啊,拉五趟比拉两趟费劲多了T_T)
原则定出来思路就出来了。原则一二基本废话,是地球人都能想到。一看原则三四,说明每到一个节点就应该损失一个车辆负载(不能不损失煤吧,是满足原则四的),这里到第一个节点时损失1000的煤拉了五趟单程,当然就在200处了。后面同理,再损失1000拉三趟单程,就到533.33处了,这时还有1000的煤。规律就是这样简单,原则想通就好。
打住,完!~zZ
三千吨的煤,搭上一列火车,费了很多劲,最后送达500吨到市场。如果我是煤老板,肯定不会同意这么干。因为这500吨要买多少钱才能把成本赚回来?定价太高了能卖出去吗?如果卖不出去还不如放在矿区算了。呵呵。我觉得程序员的算法不管多么高超,也不能忘记解决问题的目的是要提供社会价值。
x点是200,从200的点到y点,消耗煤应该是y-200。火车第二次到达y点时站点有存煤1400-2y,火车有煤1200-y,共计2600-3y,y点应该是533。最后,从y点出发,1000吨的煤,消耗467,到达目的地后,剩下煤533。我是这么分析的,不知道对不对,求赐教。@aoneatwo
受教了,我只想到了500。另外我想说的是博主的文章非常不错,是我看过的最好中文技术类博客之一,每读一篇,都有共鸣,继续关注。
重载火车可以头尾都有火车头的,题目改改重载火车每公里1吨,空载火车每公里0.7,大家哭去吧
var t=3000; //total coals
var y; //final left coals
var s=1000; // distance
var c=1; //per consume per mile
var b=1000; // most volume per travel;
var n = Math.floor(t/b);
console.log(“n = ” + n);
var a = new Array(); // for store n stage’s movement distance
a[0] = (t – n * b) / (2 * n + 1); // for per travel full volume, first consume the remainder coals
var i = 1;
var sum = a[0];
/*find the final*/
while (sum < s )
{
a[i] = b/(2 * (n-i+1) – 1);
sum += a[i];
i++;
}
console.log("i = " + i);
console.log("sum = " + sum);
var Consume = 0;
/*前i-1次运输消耗量*/
for (var j = 0; j < i-1; j++) {
console.log("第"+ (j+1) +"运输距离:"+ a[j]);
Consume += a[j]*(2 * (n-j+1) – 1);
}
console.log("前"+ (i – 1) +"次运输消耗量"+Consume);
/*前i次总运输消耗量*/
Consume += (2*(n-i+2)-1)*(a[i-1]-(sum – s));
console.log("前"+i+"次总运输消耗量"+Consume);
y = t – Consume;
console.log("终点剩余煤炭数: " + y);
程序还没写出来, 至于为什么可以这么跑也不是特清楚:
1、先运1000t煤到250km处, 放500t煤,然后返回
2、再运1000t煤到250km处, 放500t煤,然后返回
3、再运1000t煤到500km处, 放250t煤,返回250km处
4、从250km处运1000t煤到500km处, 到500km处,载上250t煤
5、到1000km处, 放下500t煤。。
其实500不是最佳答案
我们采取最浪费时间的解决方案,火车前进1公里,然后放下998吨,然后回来,这样第三次到放货点的时候已经火车都走了2.5公里,用了2.5吨煤。然后继续前行1公里,放下996吨,再回来,这样还是用了2.5吨。直到我们的货物只有2000吨的时候,我们只需要1.5吨煤就可以推进1公里了。到距离只有1000吨的时候,我们每公里消耗煤1吨。这样算下来就是
1000/2.5+1000/1.5=400+666.5>1000了,所以消耗的就是400*2.5+600×1.5=1900,运到终点就是1100吨货
@paul.xu
天哪,似乎还真是这样,你的分析很有道理,得出的数值也更大,哈哈!
只有把煤搬上搬下的工人们倒霉了 :)
不对不对,超过 2000 吨时,每公里要消耗 5 吨煤,超过 1000 吨时是 3 吨煤/公里,最终结果只能运 467 吨煤到市场
虽然你们说533是最优解但是那些煤要存放还要搬上火车 这些不要成本的???,3000吨就算运出了533吨但那些人工成本 多少?你还要找地方存放谁有这么大的地方给你存放煤炭???租地方???还是自己建场地???现在煤炭多少钱一吨???如果你是老板你怎么考虑额外的成本计算???
function geta1X(a0, s, c, k) {//a0,初始值,s,距离,c,火车容量,k,能耗系数,
//返回值,到达目的地的剩余量
var x, dx;
x = 0;
while (a0 > c && x<s) {
dx = (a0 – c * (Math.ceil(a0 / c) – 1)) / (k * (2 * (Math.ceil(a0 / c) – 1) + 1));
x += dx;
a0 = a0 – k * dx*((2 * (Math.ceil(a0 / c) – 1) + 1));
alert("这一次将所有煤运送到离出发点" + x+";剩余煤"+a0); //中间结果
}
return c – (s – x) * k; //最终结果
}
var r = geta1X(3000, 1000, 1000, 1);
alert(r);
var r = geta1X(3500, 1200, 800, 0.5); //
alert(r);
这里是最后一个例子的结果:{
这一次将所有煤运送到离出发点66.66666666666667;剩余煤3200
这一次将所有煤运送到离出发点295.23809523809524;剩余煤2400
这一次将所有煤运送到离出发点615.2380952380952;剩余煤1600
这一次将所有煤运送到离出发点1148.5714285714284;剩余煤800
最终774.2857142857142}
原发于CSDN 博客。
http://blog.csdn.net/wzhiyuan/article/details/8064577
另外,经常看楼主的博客,受益非浅。
后来又研究了一下,我上面说的不完全正确,在最后一次不需要返回的情况下,用这个公式可以的,如果需要返回,只有用我博客中说的极限公式了。
function geta1(a0, s, dx, c, k) {
var a1;
for (var i = 0; i < s / dx; i++) {
a1 = a0 – k * dx * (2 * (Math.ceil(a0 / c) – 1) + 1);
a0 = a1;
}
return a1;
}
// alert(geta1(3000, 1000, 0.1, 1000, 1));
// alert(geta1(5000, 10, 0.1, 1000, 1));
不好意思,又来了。我最后研究了一下,发现原来的例子出错了,
最终结果如下,
function geta1X2(a0, s, c, k) {
var x, dx;
x = 0;
while (a0 > c && x s){
dx = s-x;
}
a0 = a0 – k * dx * ((2 * (Math.ceil(a0 / c) – 1) + 1));
x += dx;
alert(“这一次将所有煤运送到离出发点” + x + “;剩余煤” + a0); //中间结果
}
return a0; //最终结果
}
geta1X2(5500,700,1000,0.5);
结果如下,
这一次将所有煤运送到离出发点90.9090909090909;剩余煤5000
这一次将所有煤运送到离出发点313.13131313131316;剩余煤4000
这一次将所有煤运送到离出发点598.8455988455989;剩余煤3000
这一次将所有煤运送到离出发点700;剩余煤2747.1139971139974
如果博主看到,将我无用的上面两条删除吧。谢谢。
经常在博主这里看文章,非常受益。
最好要加上考虑火车空载的耗煤量
@aoneatwo
2000-3y=1000,算出来结果应该不是333,因为当y=333时, 最后一车的吨数为2000-3y=1001,这个吨数大于一车的容量,一车装不下,那么最后一步就不能成功执行
一看到这题粗略想一想发现可能是道物理题:
如果煤老板守时是真命题的话,假定 火车 的速度为匀速。那么:
水平方向受力平衡:有
μMg = F牵
可见牵引力和火车的重量是成正比关系,而
W = F牵 * S
所以火车消耗的能量与重量是有关系的。 假定“每一公里需要耗一吨煤”是满载时所消耗的能量,那么,这时:
P = (1000kg * q J/kg)/(1000m/v m/s) = vq W
而P = F牵 * v 联立第一个公式,于是:
μMg = q
汗,煤炭的热值是固定的(原煤 20934千焦/公斤),μ 受材料本身因素影响而不变。M是给定的,那么我们可以求出
μ = 0.00214,gg了下发下这摩擦系数是低于正常值的(http://zhidao.baidu.com/question/130489014.html)。
钻个牛角尖,这毕竟是道面试题~ 工程上真要做的话就得先积分了。领悟这道题精髓就行了:)
看图吧==》结果 500 ,想不出比这更好
http://imgur.com/wzDj4
@Submarine
其实我一直纠结于为什么需要把两个中间点一个设为2000 一个设为1000. 想了想是因为每一次需要满载才能达到最优。
@gsong
800 300的时候你扔了100.那肯定就不是最优了
呵呵,这题目其实很有哲理,人的懂得回头啊~
大概与以前一个过桥类题目有点相似思路,大概意思是,一座桥长1500米,你2分钟最多走800米,桥中间每两分钟都有人出来看下,发现有人在走,立马让他回头阻止他过桥。