前两天发布那个rsync算法后，想看看数据压缩的算法，知道一个经典的压缩算法Huffman算法。相信大家应该听说过 David Huffman 和他的压缩算法—— Huffman Code，一种通过字符出现频率，Priority Queue，和二叉树来进行的一种压缩算法，这种二叉树又叫Huffman二叉树 —— 一种带权重的树。从学校毕业很长时间的我忘了这个算法，但是网上查了一下，中文社区内好像没有把这个算法说得很清楚的文章，尤其是树的构造，而正好看到一篇国外的文章《A Simple Example of Huffman Code on a String》，其中的例子浅显易懂，相当不错，我就转了过来。注意，我没有对此文完全翻译。

我们直接来看示例，如果我们需要来压缩下面的字符串：

 “beep boop beer!” 

首先，我们先计算出每个字符出现的次数，我们得到下面这样一张表 :

字符	次数
‘b’	3
‘e’	4
‘p’	2
‘ ‘	2
‘o’	2
‘r’	1
‘!’	1

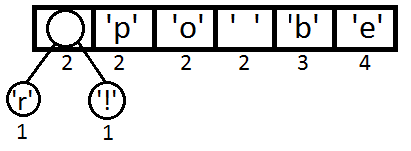
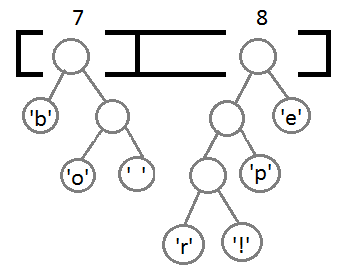
然后，我把把这些东西放到Priority Queue中（用出现的次数据当 priority），我们可以看到，Priority Queue 是以Prioirry排序一个数组，如果Priority一样，会使用出现的次序排序：下面是我们得到的Priority Queue：

接下来就是我们的算法——把这个Priority Queue 转成二叉树。我们始终从queue的头取两个元素来构造一个二叉树（第一个元素是左结点，第二个是右结点），并把这两个元素的priority相加，并放回Priority中（再次注意，这里的Priority就是字符出现的次数），然后，我们得到下面的数据图表：

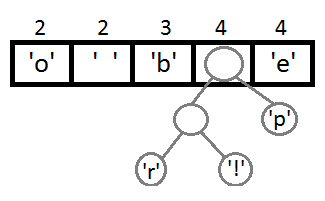
同样，我们再把前两个取出来，形成一个Priority为2+2=4的结点，然后再放回Priority Queue中 :

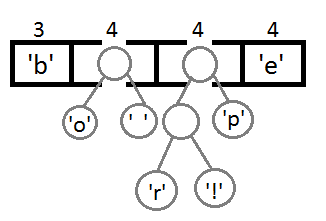
继续我们的算法（我们可以看到，这是一种自底向上的建树的过程）：

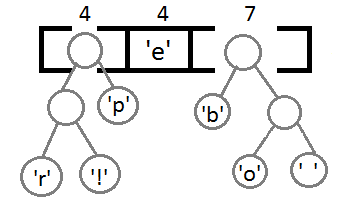
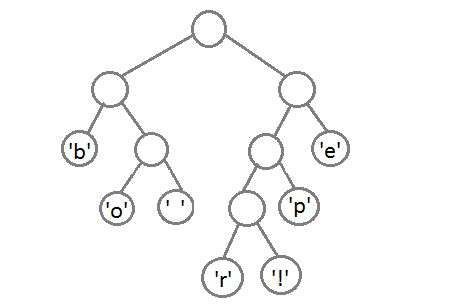
最终我们会得到下面这样一棵二叉树：

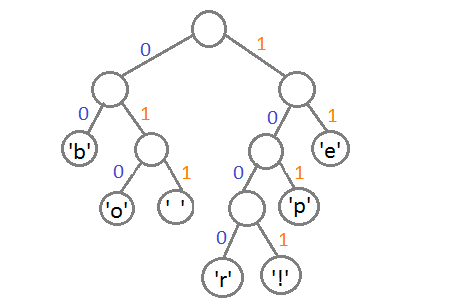
此时，我们把这个树的左支编码为0，右支编码为1，这样我们就可以遍历这棵树得到字符的编码，比如：‘b’的编码是 00，’p’的编码是101， ‘r’的编码是1000。我们可以看到出现频率越多的会越在上层，编码也越短，出现频率越少的就越在下层，编码也越长。

最终我们可以得到下面这张编码表：

字符	编码
‘b’	00
‘e’	11
‘p’	101
‘ ‘	011
‘o’	010
‘r’	1000
‘!’	1001

这里需要注意一点，当我们encode的时候，我们是按“bit”来encode，decode也是通过bit来完成，比如，如果我们有这样的bitset “1011110111″ 那么其解码后就是 “pepe”。所以，我们需要通过这个二叉树建立我们Huffman编码和解码的字典表。

这里需要注意的一点是，我们的Huffman对各个字符的编码是不会冲突的，也就是说，不会存在某一个编码是另一个编码的前缀，不然的话就会大问题了。因为encode后的编码是没有分隔符的。

于是，对于我们的原始字符串  beep boop beer!

其对就能的二进制为 : 0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 0001

我们的Huffman的编码为： 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001

从上面的例子中，我们可以看到被压缩的比例还是很可观的。

作者给出了源码你可以看看（ C99标准） Download the source files

（全文完）